ต้องขอบอกว่า Happy Birthday ออยเลอร์ ถ้าเขายังมีชีวิตอยู่ เขาจะมีอายุถึง 306 ปี แล้ว! (จริงๆ ไม่ถือว่าห่างจากยุคปัจจุบันเท่าไหร่ เมื่อเทียบกับนักคณิตศาสตร์ หรือนักวิทยาศาสตร์บางท่าน) แต่ต้องบอกว่าหลังจากมีตานี่โผล่ขึ้นมาบนโลก คณิตศาสตร์ก็ยากขึ้นทันที ไม่เชื่อก็ลองดูโจทย์โอลิมปิกสิ โอ้วมายกอด
เขียนมาถึงตรงนี้ หลายคนยังงงอยู่ ออยเลอร์ เป็นใคร? จริงๆแล้วน้องๆ ม.ปลาย อาจจะหลง งง เสียตัวกับ ตาออยเลอร์มาตั้งแต่ ม. 4 แล้ว (ต๊าย! ใจง่ายนะหล่อน) แค่เรื่อง เซต ก็เจอแล้วจริงไม๊ แผนภาพของเวนน์-ออยเลอร์ ไง
พอขึ้นม. 5 ก็ต้องต้องเสียตัวให้กับตาออยเลอร์อีกครั้ง เรื่องเอกซ์โพเนนเชียลและลอกาลิธึม ม. 6 ถ้าใครได้เรียน diff ขั้นสูงหน่อย ก็จะเจอตาออยเลอร์อีกละ
เรียกได้ว่า ออยเลอร์ เป็นคนสำคัญจริงๆ เราต้องพบพาน เวียนว่ายตายเกิดกับตานี่พอสมควร เอาละๆ ไหนๆก็ไหนๆแล้ว มารู้จักกับ ออยเลอร์ ว่าเป็นใคร?
Leonhard Euler
เป็นไงล่ะ เห็นภาพและประวัติย่อแล้วถึงกับอึ้งกิมกี่ไปเลย ....... เพราะว่าแปลไม่ออก
เผอิญพี่ก็จบมาจากต่างประเทศซะด้วย ก็เลยแบบว่า ชิวๆอ่ะ คือแบบว่า เหมือนภาษาบ้านเกิด ก็เลยแปลออกง่ายๆ (เริ่มเลอะเทอะ)
ก็จะบอกให้เอาบุญ ชื่อของเขาคือ เลโอนาร์ด ออยเลอร์ เป็นนักคณิตศาสตร์และฟิสิกส์ ชาวสวิสเซอร์แลนด์ เขาได้ค้นพบเรื่องราวมากมายหลายอย่างทางด้านแคลคูลัสและทฤษฎีกราฟ
เพิ่มเติมอีกหน่อย ออยเลอร์ เนี่ยเป็นคนที่ "ติสแตก" พอสมควร เขาเป็นคนแรกที่ใช้คำว่า ฟังก์ชัน โดยอ้างอิงนิยามของ ไลบ์นิซ (ตัวละครลับอีกตัวละ ช่างมันก่อนละกัน) และยังเป็นผู้ที่ทารุณนักฟิสิกส์ โดยการเอาแคลคูลัส ไปผูกกับการคำนวณต่างๆของฟิสิกส์อีกด้วย (พาเขายุ่งวุ่นวายไปหมด)
ด้วยความอัจฉริยะ ทำให้เขามีผลงานที่ตีพิมพ์ออกมามากกว่า 75 เล่ม (ในสมัยนั้นถือว่าเยอะมาก เพราะว่าการจะตีพิมพ์อะไรสักอย่าง ต้องเป็นสิ่งใหม่เท่านั้น)
แต่ความอัจฉริยะ ก็มาพร้อมกับชะตากรรม ประหนึ่งพระเอกที่่ต้องพบพานกับอุปสรรค ออยเลอร์สูญเสียการมองเห็นไปในช่วงศตวรรษที่ 18 เป็นเวลา 17 ปี ก่อนจะจบชีวิตลง แต่ช่วงที่เขามองไม่เห็น กลับสร้างสรรค์ผลงานได้เกือบครึ่งจากผลงานทั้งหมด
คือพี่ไม่แน่ใจว่าไอ้ที่ว่าสูญเสียการมองเห็นเนี่ย มันเสียไปข้างเดียวหรือเปล่า? ถึงได้สร้างผลงานได้มากมายเช่นนั้น (คือถ้าดูจากรูปแล้วน่าจะข้างเดียวมากกว่าคือ ตาขวา)
พอมาในยุคปัจจุบัน ปี 2002 มีการค้นพบดาวเคราะห์น้อยกลุ่มนึง จึงได้ตั้งชื่อเพื่อเป็นเกียรติแก่ออยเลอร์ว่า "ดาวเคระห์น้อย 2002 ออยเลอร์" (ตั้งชื่อสิ้นคิดจริงๆน่ะแหละ)
แต่ต้องบอกก่อนว่า ทฤษฎีของออยเลอร์ บางอัน ถูกหักล้างไปหลายๆงานเหมือนกัน บางทีออยเลอร์ก็คิดตื้นไป โดยพิสูจน์น้อยครั้งเกินไป ทำให้เป็นช่องให้นักคณิตศาสตร์รุ่นหลังๆ เพราะสมัยใหม่ๆ เรานำคอมพิวเตอร์มาช่วยคำนวณนั่นเอง (คอมพิวเตอร์เทพกว่าคนเสียอีก)
ทีนี้ มาดูตัวอย่างผลงานของออยเลอร์ ที่เราเจอกันใน ม.ปลาย กันดีว่า ถ้าน้องๆจำได้ ในเรื่องจำนวนเชิงซ้อน การเขียนจำนวนเชิงซ้อนในรูปเชิงขั้ว พี่จะแถมการเขียนเชิงขั้วแบบ ของออยเลอร์ด้วย

และบอกด้วยว่า มีกรณีนึงเราเรียกว่า เป็นเอกลักษณ์เชิงขั้วของออยเลอร์ คือ
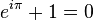
นอกจากนี้ผมงานเขายังมีอีกมากมายก่ายกอง แต่อย่างที่บอก คือใช้ได้บ้างไม่ได้บ้าง ปนๆกันไป นับว่าเป็นนักคณิตศาสตร์ที่มีคนพยายามจะหักล้างทฤษฎีของเขา พอๆกับพิทากอรัส เลยก็ว่าได้
แต่ยังไงซะเขาก็เป็นนักคณิตศาสตร์ที่น่าทึ่ง และทำให้เราเรียนได้ยากขึ้นอย่างน่าอัศจรรย์ (เอ๊ะยังไง?)
สุดท้ายนี้ ก็ขออวยพรวันเกิดครบรอบ 306 ปี ด้วยนะครับ ถ้าไม่มีออยเลอร์ ผมก็คงไม่ได้มาสอนคณิตศาสตร์อย่างทุกวันนี้จริงๆ T T
เผอิญพี่ก็จบมาจากต่างประเทศซะด้วย ก็เลยแบบว่า ชิวๆอ่ะ คือแบบว่า เหมือนภาษาบ้านเกิด ก็เลยแปลออกง่ายๆ (เริ่มเลอะเทอะ)
ก็จะบอกให้เอาบุญ ชื่อของเขาคือ เลโอนาร์ด ออยเลอร์ เป็นนักคณิตศาสตร์และฟิสิกส์ ชาวสวิสเซอร์แลนด์ เขาได้ค้นพบเรื่องราวมากมายหลายอย่างทางด้านแคลคูลัสและทฤษฎีกราฟ
เพิ่มเติมอีกหน่อย ออยเลอร์ เนี่ยเป็นคนที่ "ติสแตก" พอสมควร เขาเป็นคนแรกที่ใช้คำว่า ฟังก์ชัน โดยอ้างอิงนิยามของ ไลบ์นิซ (ตัวละครลับอีกตัวละ ช่างมันก่อนละกัน) และยังเป็นผู้ที่ทารุณนักฟิสิกส์ โดยการเอาแคลคูลัส ไปผูกกับการคำนวณต่างๆของฟิสิกส์อีกด้วย (พาเขายุ่งวุ่นวายไปหมด)
ด้วยความอัจฉริยะ ทำให้เขามีผลงานที่ตีพิมพ์ออกมามากกว่า 75 เล่ม (ในสมัยนั้นถือว่าเยอะมาก เพราะว่าการจะตีพิมพ์อะไรสักอย่าง ต้องเป็นสิ่งใหม่เท่านั้น)
แต่ความอัจฉริยะ ก็มาพร้อมกับชะตากรรม ประหนึ่งพระเอกที่่ต้องพบพานกับอุปสรรค ออยเลอร์สูญเสียการมองเห็นไปในช่วงศตวรรษที่ 18 เป็นเวลา 17 ปี ก่อนจะจบชีวิตลง แต่ช่วงที่เขามองไม่เห็น กลับสร้างสรรค์ผลงานได้เกือบครึ่งจากผลงานทั้งหมด
คือพี่ไม่แน่ใจว่าไอ้ที่ว่าสูญเสียการมองเห็นเนี่ย มันเสียไปข้างเดียวหรือเปล่า? ถึงได้สร้างผลงานได้มากมายเช่นนั้น (คือถ้าดูจากรูปแล้วน่าจะข้างเดียวมากกว่าคือ ตาขวา)
พอมาในยุคปัจจุบัน ปี 2002 มีการค้นพบดาวเคราะห์น้อยกลุ่มนึง จึงได้ตั้งชื่อเพื่อเป็นเกียรติแก่ออยเลอร์ว่า "ดาวเคระห์น้อย 2002 ออยเลอร์" (ตั้งชื่อสิ้นคิดจริงๆน่ะแหละ)
แต่ต้องบอกก่อนว่า ทฤษฎีของออยเลอร์ บางอัน ถูกหักล้างไปหลายๆงานเหมือนกัน บางทีออยเลอร์ก็คิดตื้นไป โดยพิสูจน์น้อยครั้งเกินไป ทำให้เป็นช่องให้นักคณิตศาสตร์รุ่นหลังๆ เพราะสมัยใหม่ๆ เรานำคอมพิวเตอร์มาช่วยคำนวณนั่นเอง (คอมพิวเตอร์เทพกว่าคนเสียอีก)
ทีนี้ มาดูตัวอย่างผลงานของออยเลอร์ ที่เราเจอกันใน ม.ปลาย กันดีว่า ถ้าน้องๆจำได้ ในเรื่องจำนวนเชิงซ้อน การเขียนจำนวนเชิงซ้อนในรูปเชิงขั้ว พี่จะแถมการเขียนเชิงขั้วแบบ ของออยเลอร์ด้วย

และบอกด้วยว่า มีกรณีนึงเราเรียกว่า เป็นเอกลักษณ์เชิงขั้วของออยเลอร์ คือ
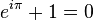
นอกจากนี้ผมงานเขายังมีอีกมากมายก่ายกอง แต่อย่างที่บอก คือใช้ได้บ้างไม่ได้บ้าง ปนๆกันไป นับว่าเป็นนักคณิตศาสตร์ที่มีคนพยายามจะหักล้างทฤษฎีของเขา พอๆกับพิทากอรัส เลยก็ว่าได้
แต่ยังไงซะเขาก็เป็นนักคณิตศาสตร์ที่น่าทึ่ง และทำให้เราเรียนได้ยากขึ้นอย่างน่าอัศจรรย์ (เอ๊ะยังไง?)
สุดท้ายนี้ ก็ขออวยพรวันเกิดครบรอบ 306 ปี ด้วยนะครับ ถ้าไม่มีออยเลอร์ ผมก็คงไม่ได้มาสอนคณิตศาสตร์อย่างทุกวันนี้จริงๆ T T







